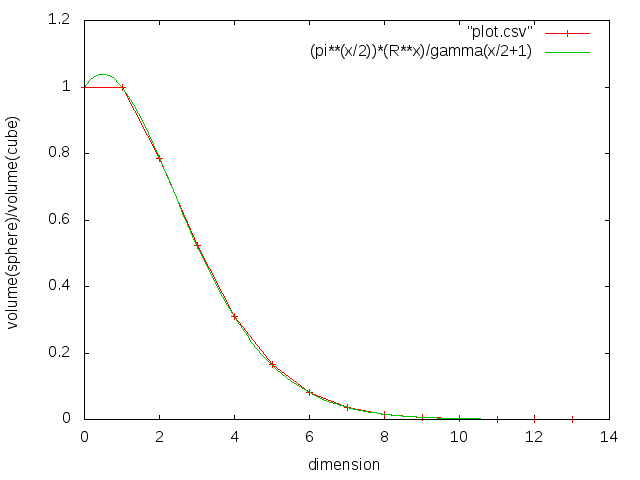
Volume of Spheres to Cubes Over Varying Dimensions.

As James Jolly said(approximately) to me, as the number of dimensions goes up, a normally-distributed dataset's points become closer together. To approximate it, draw a circle in a square, followed by a sphere in a cube, followed by a hypersphere in a hypercube. This relationship wasn't intuitively apparent to me, so I plotted it out. This is also known as the curse of dimensionality.

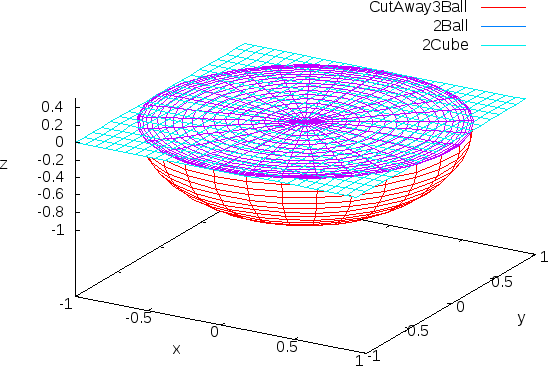
To think recursively, each next-higher dimension contains an infinitely thin slice of the current dimension. For example, in three dimensions, a the area of a circle cut through a unit sphere by a plane of z=0 is the same area as a 2-dimesional unit circle. This is true all the way down - a 1-dimensional circle fills the 1-dimensional space from the leftmost to the righmost points on the 2-dimensional circle.

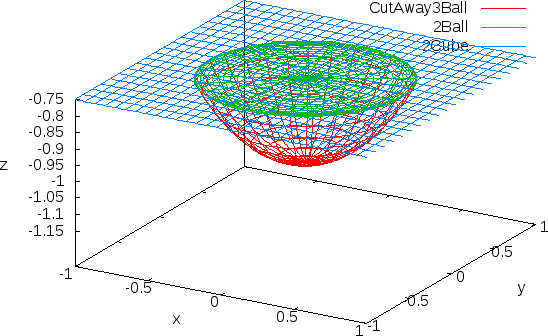
But, we may notice that the ratio of circle-to-square in our slice is highest only in the middle(z=0). By varying from the center of our dimension-splitting subregion that ratio in the slice is always smaller. This is also true for the ratio of sphere-to-square in any two neighboring dimension sets(n->n+1). By approximating an integral, if the highest ratio in a dimensional space is the ratio in the lower dimensional space, and our integral averages over all the current space, then the ratio in the current space must go down, as being an average of ranges between 0 and the ratio of the previous space.