Graphical Analysis of Collision Rates of Various CRCs

Introduction

CRCs, or Cyclic-Redundancy-Check, are a simple sort of hash function commonly used to detect accidental changes in data. Recently, I took a few English-language word-lists, and plotted the collision rates of various CRC and related checksum algorithms. Wikipedia lists 48 different CRCs, but this graph will show collision rates of several 16-bit functions and two 32-bit functions.

Purpose of CRCs

CRCs are commonly used for two purposes. They are often used as a redundant(data added without information) few bytes added to a packet to evaluate integrity, but they can also be used as a hash function to give a fixed-length integer value as a summary or index for various-length inputs. Today we will look at them purely as hash functions.

Data Set

For today, we will be using a combination of two wordlists, with repetitions filtered out. The file is 3904690 bytes long with 374009 words. The average word is 9.4 letters long. One weakness in this dataset is the lack of long inputs - word lists contain many short records but some functions perform poorly on short records and require a certain minimum input before performing well.

How to read the graph

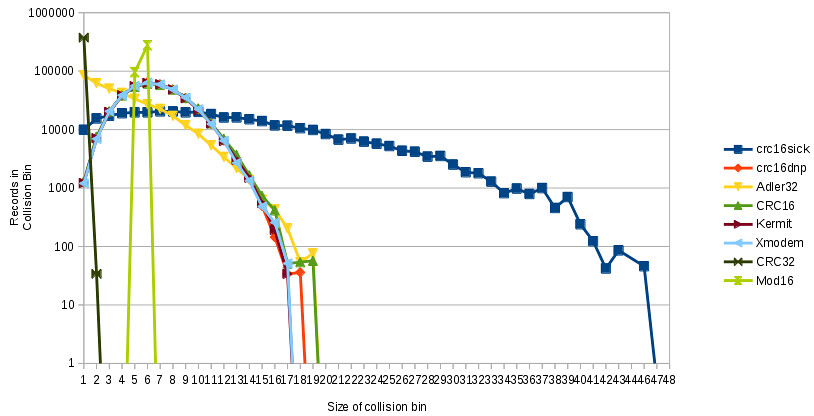
On this graph, collisions are binned into groups. All collisions over the file where exactly three items collided into the same hash slot, are drawn over bin three.

On the X-Axis this graph shows the number of records per collision, and on the Y-Axis it shows how many records were in each collision. So, the number of records in X-collision slot 1 represents the number of records without any collisions, and the number of records in slot 46 shows that there were 46 records in that collision slot for CRC16SICK.

Finally, the Y-Axis of this graph is scaled on a log-curve. This allows us to plot CRC32, which has very few collisions, on the same graph as CRC16SICK, which has many collisions, and make sense of it. On a linear graph, CRC32 would blow everything else out of the scale.

It is also possible to redraw this graph plotting on the Y-Axis the number of times each collision bin was counted - for the same dataset, that graph would have a Y-Axis value of one in slot 46. But, this graph has the advantage that if rendered on a linear graph, the area under each curve would be the same.

What does a good function look like?

On this graph, a good function will have as few collisions as possible, so it'll be centered toward the left. However, if the output space is constrained smaller than the number of inputs, the center will necessarily be shifted to the right. Under these conditions, good functions will keep the collision distribution close to a perfect one, which is a narrow bar centered on the number of inputs divided by the number of outputs.

16-Bit Functions

16-bit functions have an output space of 65536 slots, so a perfect hash function modulo 65536 would yield collisions of either 5 or 6 for every collided value. These hashes are two bytes long.

Mod16

Mod16 represents a minimal perfect hash mod 65536. Although functions like this can be designed for known input spaces, CRCs are designed to work on general-purpose inputs, so consider this curve just a reference for the best a 16-bit function could do.

True 16-bit CRCs: Kermit, CRC16, CRC16DNP, XMODEM

These are all 16-bit CRCs with possibly varying polynomials. They all form curves approximately peaked near the expected values of either 5 or 6 with lesser amounts of records in larger and smaller bins. These make good use of their limited 16-bit output spaces.

CRC16SICK

SICK is a sensor company known for Lidar and other optical sensors. They use a 16-bit CRC-like function, seemingly optimized for speed. However, on this dataset, it performs poorly as a hash function with 46 inputs mapped to the same output in some cases, and nearly 10,000 inputs uniquely mapped. This is the least balanced hash function, although it likely was not design for hash function usage.

32-Bit Functions

32-bit hash functions have an expected output space of approximately 4 billion records, so a perfect hash function would have no collisions on data sets of this size. Also, these hashes take 4 bytes to store.

CRC32

CRC32 does a great job on this input set; however, it does have a significantly larger output space to work in. At the cost of 4-byte hashes, this is the best function evaluated.

Adler32

Adler32 is a particular derivation of Fletcher32, which attempts to perform close to CRC32 for error detection while being simpler and faster to calculate. However, Adler32 does not perform well on short inputs, which this dataset consists of. While simpler to calculate than CRC32, as a hash Adler32 seems better than all 16-bit functions, but still comes with the cost of 32-bit output hashes.