ArduPilot: A Matter of Time
Written 2024-02-04
Tags:ArduPilot Floating-point
I have a couple of drones and an RC car controlled by a custom PCB I made with a RaspberryPi running OpenHD and ArduPilot. It's fun to play with when I have time.
Recently, I left one of my drones powered with the props removed while I was replacing a desk in my office. A surgery and some shaved yak's later, the old desks are gone, the new desk surface doesn't fit around a hallway corner, I'm building a new desk surface with a friend, and the drone has been plugged in the whole time, rebooting only for power outages.
When I finally checked in on it, the Linux OS seemed fine, but some periodic ArduPilot code I was tracing was reporting very strange timestamps - every timestamp was rounded to 1/4 second, or 250 milliseconds.
The root cause was a couple events:
- The initial ArduPilot HAL for Linux in 2013 uses default-precision(double at the time) floats for converting between Linux timevals & timespecs and ArduPilot millis() & micros().
- Last summer ArduPilot switches from double-precision to single-precision float litterals with -fsingle-precision-constant. It's important to note that ArduPilot targets mostly microcontrollers, some with only single-precision FPUs, where double-precision math is expensive.
- I happened to leave my board running long enough for rounding and conversion errors to be obvious.
Here's the offending code:
uint64_t micros64()
{
const Linux::Scheduler* scheduler = Linux::Scheduler::from(hal.scheduler);
uint64_t stopped_usec = scheduler->stopped_clock_usec();
if (stopped_usec) {
return stopped_usec;
}
struct timespec ts;
clock_gettime(CLOCK_MONOTONIC, &ts);
return 1.0e6*((ts.tv_sec + (ts.tv_nsec*1.0e-9)) -
(state.start_time.tv_sec +
(state.start_time.tv_nsec*1.0e-9)));
}
With the double-precision constants and calculations in-use at the time, the rounding errors were very small, most notably some microseconds were only 999 nanoseconds long, but this wasn't very often if Linux and ArduPilot hadn't been running too long. After the change to 32-bit floats, things come apart quickly.
First, 1.0e-9 isn't an exact 32-bit number, so it gets rounded to about .9999999974752427078783512115478515625e-6 - this isn't really an issue, because it would only be responsible for around 80ns/year of clock drift, and only affects the fractional seconds count, so the drift re-aligns every new second.
I'll also define a term here, ArduPilot epoch - it's the millis() or micros() since ArduPilot read the start_time from Linux. There's also Linux's CLOCK_MONOTONIC epoch, which is seconds and nanoseconds since the Linux system startup, possibly with NTP skewing.
We next need to consider the order of addition and subtraction operations above - we're taking seconds plus fractional nanoseconds, and subtracting from that seconds plus fractional nanoseconds. This means that we need a precise enough representation to hold both seconds and nanoseconds combined, and a 32-bit float is often good for about 6-7 decimal digits, but a second is 10e9 nanoseconds. A partial improvement here would be add the difference of nanoseconds to the difference of seconds, this way the differences are first computed exactly. This would allow ArduPilot to compute the difference from CLOCK_MONOTONIC epoch to ArduPilot epoch exactly, but as ArduPilot runs longer things still get weird.
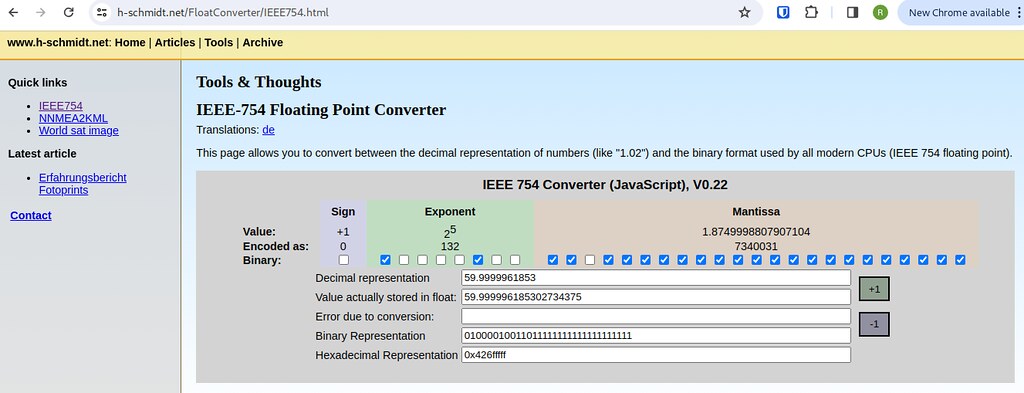
Finally, we should look directly at the 32-bit floating-point datatype. I really like this calculator for playing with 32-bit float quantization and rounding issues. At this middle part of micros64(), where we're dealing with floating-poing seconds since ArduPilot startup, if we want to calculate floating-point resolution at say, 60 seconds of ArduPilot epoch, enter 60 into the calculator and hit '-1' to compute the next lowest 32-bit floating-point number, we get a number that is ~4 microseconds away from 60. This means that calling micros() around 1 minute after ArduPilot startup can be off by up to 4 microseconds.
Things quickly get weirder the longer the system runs, or the later ArduPilot is started after Linux:
| Approx epoch | Approx representation error |
|---|---|
| 1 second | 60 nanoseconds |
| 1 minute | 4 microseconds |
| 1 hour | 244 microseconds |
| 1 day | 8 milliseconds |
| 1 week | 62.5 milliseconds |
| 3 weeks | 125 milliseconds |
| 1 month | 250 milliseconds |
| 2 months | 500 milliseconds |
| 4 months | 1 second |
| 6 months | 1 second |
| 8 months | 2 seconds |
| 1 year | 2 seconds |
| 14 years | 2038 bug! |
It's neat that we can see the floating-point format at play here. As the epoch runs on, the floating-point error goes up, but the time between increases in floating-point error go up too. This makes sense because each time the floating-point moves up, the space between representable numbers increases. Granularity of time tends to cause measurement errors where one interval might seem short (because it contains fewer time ticks) or another seem long(because it has an extra time tick). At an extreme, intervals of 0 ticks are instant. What sort of practical issues can this cause? We can run one of ArduPilot's test programs for just this! Here's output from the Scheduler_test around 3 weeks of Linux uptime, 1 minute of ArduPilot uptime, t= milliseconds since Scheduler_test launch:
five_seconds: t=53375 ins_counter=3750 one_hz: t=54000 one_hz: t=54500 one_hz: t=55000 one_hz: t=55500 one_hz: t=56000 five_seconds: t=56000 ins_counter=4000
The fp32 rounding error is quite obvious. But also note that the Scheduler is running the one_hz task at 2Hz. Here's an example of where problems can occur when millis64() might increment by 8 milliseconds after a day of uptime:
void Scheduler::delay(uint16_t ms)
{
if (_stopped_clock_usec) {
return;
}
uint64_t start = AP_HAL::millis64();
while ((AP_HAL::millis64() - start) < ms) {
// this yields the CPU to other apps
microsleep(1000);
if (in_main_thread() && _min_delay_cb_ms <= ms) {
call_delay_cb();
}
}
}
After a day of uptime, a simple delay(1ms) will either delay execution between 0ms and 8ms depending on when delay() is called relative to when the floating-point time increments.
I had started on a couple patches to move back to double-precision math and reorder operations, but Andrew Tridgell beat me to it, using uint64_t nanoseconds and an optimized integer division routine.